sklearnを使って重線形回帰やってみた
過去の投稿と同様の計算をするのですが、以下の点を変更してみました。
1, sklearnを使うこと
2, 入力(独立変数)の標準化を行うこと
ライブラリのインポート
In [1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from sklearn.linear_model import LinearRegression
データの読み込み
In [2]:
data = pd.read_csv('mibile_company_stock_price_2020-10-01_2021-09-30.csv')
data.head()
Out[2]:
In [3]:
data.describe()
Out[3]:
回帰モデルの作成
従属変数と独立変数の宣言
In [4]:
x = data[['KDDI','softbank','rakuten']]
y = data['NTT']
入力の標準化
In [5]:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(x)
x_scaled = scaler.transform(x)
回帰の実行
In [6]:
reg = LinearRegression()
reg.fit(x_scaled,y)
Out[6]:
切片の表示
In [7]:
reg.intercept_
Out[7]:
係数の表示
In [8]:
reg.coef_
Out[8]:
標準化しなかったときと標準化したときの切片と係数を比較すると以下の通り
| 標準化しない時 | 標準化した時 | |
| 切片 | -588.0258 | 2679.66391752 |
| KDDIの係数 | 0.4863 | 118.41334058 |
| softbankの係数 | 1.0179 | 86.45023339 |
| rakutenの係数 | 0.2364 | 37.72179729 |
決定係数は変わらないのだが、標準化するとどの入力(独立変数)が重要かがわかる。今回の場合は、KDDIの係数が重要であることがわかる
決定係数の計算
In [9]:
reg.score(x_scaled,y)
Out[9]:
自由度修正済み決定係数の公式
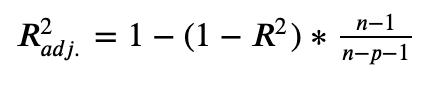
自由度修正済み決定係数の計算
In [10]:
def adj_r2(x,y):
r2 = reg.score(x,y)
n = x.shape[0]
p = x.shape[1]
adjusted_r2 = 1-(1-r2)*(n-1)/(n-p-1)
return adjusted_r2
In [11]:
adj_r2(x_scaled,y)
Out[11]:
予測
In [12]:
new_data = [[3000,1500,1000]]
new_data_scaled = scaler.transform(new_data)
In [13]:
reg.predict(new_data_scaled)
Out[13]:
それぞの変数のp値の計算
それぞの変数のp値の計算¶
In [14]:
from sklearn.feature_selection import f_regression
In [15]:
f_regression(x_scaled,y)
Out[15]:
In [16]:
p_values = f_regression(x,y)[1]
p_values
Out[16]:
In [17]:
p_values.round(3)
Out[17]:
In [18]:
reg_summary = pd.DataFrame(data = x.columns.values, columns=['Features'])
reg_summary ['Coefficients'] = reg.coef_
reg_summary ['p-values'] = p_values.round(3)
reg_summary
Out[18]:
全てのP値が0.05を下回っていることから、標準化しなかった時と同様、全ての入力(独立変数)が優位な影響があることがわかります。






ディスカッション
コメント一覧
まだ、コメントがありません